Глава VIII. Дедуктивные умозаключения.
1. Что такое умозаключение?
Умозаключение — это такое логическое действие, посредством которого из двух или нескольких логически связанных суждений мы получаем новое суждение. Причём, если наши изначальные суждения истинны и если мы правильно применяем к ним законы логики, то новое суждение будет верным.
2. Дайте определение силлогизма.
Силлогизм, или дедуктивное умозаключение, — это такое умозаключение, в котором из двух данных суждений выводится третье суждение, причём одно из двух данных суждений — непременно общее.
Категорический силлогизм — силлогизм состоящий из категорических суждений.
3. Что входит в состав силлогизма?
В состав силлогизма входят две посылки и заключение. Понятия, которые входят в состав посылок и заключения называются терминами. Терминов всего три: меньший термин (S), больший термин (Р) и средний термин (М). Названия «меньший» и «больший» возникли потому, что сказуемое обычно бывает больше по объёму, чем подлежащее. Та посылка, в состав которой входит больший термин, называется большей посылкой; та посылка, в состав которой входит меньший термин, называется меньшей посылкой.
| Состав силлогизма. | Пример силлогизма. | |
|---|---|---|
| Бóльшая посылка: | (М—Р) | Все планеты шарообразны. |
| Мéньшая посылка: | (S—М) | Земля — планета. |
| Заключение: | (S—Р) | Земля шарообразна. |
4. Назовите термины силлогизма. Укажите роль в силлогизме каждого термина.
| Обозначение термина | Чем является в составе заключения? | |
|---|---|---|
| S | Меньший термин | Подлежащее заключения |
| P | Больший термин | Сказуемое заключения |
| M | Cредний термин | Не входит в состав заключения. Является связующим звеном между посылками. |
5. Что такое аксиома силлогизма? Сформулируйте её.
Весь силлогизм в целом является отражением отношения вещей: если S (мéньшая посылка) входит в М , а М входит в Р (бóльшая посылка), то ясно, что S входит в Р (заключение).
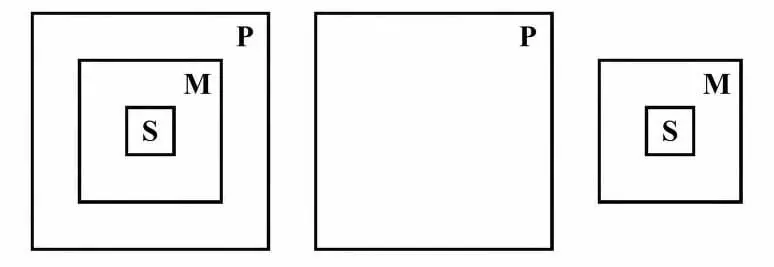
Аксиома силлогизма: Всё, что утверждается (или отрицается) относительно всего класса предметов, то утверждается (или отрицается) относительно части этого класса.
6. При каких условиях может быть истинным заключение силлогизма?
Если посылки верны и если законы логики применены правильно, то заключение должно быть истинным.
7. Назовите правила силлогизма.
Существует пять правил простого категорического силлогизма:
I. В силлогизме должно быть не больше и не меньше трёх суждений и трёх терминов.
II. Средний термин должен быть распределён хотя бы в одной из посылок.
III. Термины в заключении должны иметь тот же объём, какой они имеют в посылках.
IV. Из двух отрицательных посылок нельзя вывести заключения; если одна из посылок отрицательная, то и заключение будет отрицательным.
V. Из двух частных посылок нельзя вывести заключения; если одна из посылок частная, то и заключение будет частным.
Понятие модуса. Таблица возможных модусов.
Модусы — разновидности силлогизма образованные тем или другим сочетанием разных по количеству и качеству суждений.
Модусами являются такие сочетания суждений, которые не противоречат правилам категорического силлогизма.
Перебрав все сочетания суждений, и выбрав не противоречащие правилам, получим следующую таблицу:

8. Чем различаются фигуры силлогизма?
Средний термин может занимать в силлогизме различные положения, в зависимости от этого различают четыре фигуры силлогизма.
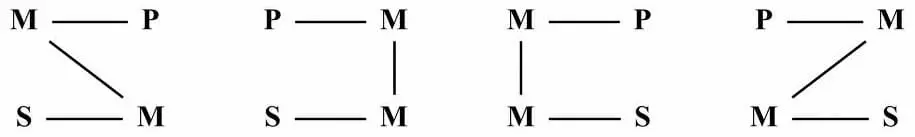
Каждая схема изображает две посылки и связь между посылками. Горизонтальные линии обозначают связь терминов в посылках, а наклонные и вертикальные линии — связь между посылками. Заключения на рисунке не показаны, так как их схема одинакова для всех фигур: S — P.
1-я фигура. Средний термин является подлежащим большей посылки и сказуемым меньшей посылки. Бóльшая посылка должна быть обязательно общей, а мéньшая — утвердительной. Первой фигурой мы пользуемся тогда, когда нам надо частный случай подвести под общее положение или же из более общего вывести менее общее.
2-я фигура. Средний термин является сказуемым в обеих посылках. Бóльшая посылка должна быть обязательно общей, а одна из посылок — отрицательной. Второй фигурой пользуются в тех случаях, когда хотят доказать, что данное явление не подходит под общее положение.
3-я фигура. Средний термин является подлежащим в обеих посылках. Мéньшая посылка должна быть обязательно утвердительной, а заключение — частным. Третья фигура применяется главным образом тогда, когда надо доказать ложность какого-либо общего положения, причём доказательство производится с помощью указания на частные случаи, которые противоречат опровергаемому общему положению.
4-я фигура. Средний термин является сказуемым большей посылки и подлежащим меньшей посылки. Данная фигура используется редко, поэтому здесь не рассмотрена.
9. Что такое условный силлогизм? (Приведите примеры.)
Условный силлогизм — это такой силлогизм, в котором, по крайней мере, одна из посылок является условным суждением.
Если в условном силлогизме одна из посылок — условное суждение, а другая — категорическое, то такой силлогизм называется условно-категорическим.
Существуют две формы условно-категорического силлогизма:
Утверждающая форма условно-категорического силлогизма:
| Общая формула. | Пример. |
|---|---|
| Если S есть P, то S1 есть P1. | Если рожь пожелтела, то её необходимо жать. |
| S есть P. | Рожь пожелтела. |
| Следовательно, S1 есть P1. | Следовательно, её необходимо жать. |
Отрицающая форма условно-категорического силлогизма:
| Общая формула. | Пример. |
|---|---|
| Если S есть P, то S1 есть P1. | Если гроза проходит далеко, то грома не слышно. |
| S1 не есть P1. | Гром слышно. |
| Следовательно, S не есть P. | Следовательно, гроза проходит недалеко. |
10. Какие две формы условного силлогизма дают достоверный вывод?
В условных умозаключениях мы получаем достоверный вывод в двух случаях:
I. По утверждающей форме, когда от утверждения основания мы переходим к утверждению следствия;
II. По отрицающей форме, когда мы от отрицания следствия переходим к отрицанию основания.
Для всех других форм условного силлогизма нет общего правила получения верного вывода, но всегда можно получить вероятный вывод — тоже полезный на практике.
11. В каких случаях мы получаем в условном силлогизме лишь вероятный вывод?
Во всех других случаях, не подходящих под утверждающую и отрицающую формы условного силлогизма.
12. Что такое разделительный силлогизм?
Разделительный силлогизм — это такой силлогизм, в котором одна или обе посылки являются разделительными суждениями.
Силлогизм, в котором одна посылка разделительная, а другая категорическая, называется разделительно-категорическим.
13. Укажите две формы разделительного силлогизма.
Утверждающая форма разделительного силлогизма:
| Общая формула. | Пример. |
|---|---|
| S есть или P1, или P2, или P3. | Данное вещество содержит в себе или хлор, или бром. |
| S не есть ни P1, ни P2. | Анализ показал, что данное вещество не содержит в себе хлора. |
| Следовательно, S есть P3 | Следовательно, оно содержит бром. |
Отрицающая форма разделительного силлогизма:
| Общая формула. | Пример. |
|---|---|
| S есть или P1, или P2, или P3. | Такие следы на снегу могла оставить или лисица, или куница. |
| S есть P1. | Установлено, что здесь оставила следы лисица. |
| Следовательно, S не есть ни P2, ни P3. | Следовательно, куница здесь следов не оставила. |
14. Укажите правила разделительного силлогизма.
I. Предикаты (P) большей посылки должны исключать друг друга. В данном случае союз «или» имеет разделительное значение.
II. Совокупность предикатов (P) большей посылки должна полностью исчерпывать объём субъекта (S) этой посылки.
15. Что такое энтимема?
Энтимема — сокращённая форма силлогизма, в которой какая-либо часть его не высказывается, а только подразумевается.
16. Укажите три вида энтимемы.
I. Силлогизм без большей посылки.
II. Силлогизм без меньшей посылки.
III. Силлогизм без заключения.
17. Для чего бывает необходимо восстановить энтимему?
Восстановить энтимему — это значит привести умозаключение к виду силлогизма со всеми его частями.
Восстановление энтимем даёт возможность обнаружить ошибку в умозаключении.
Скачать всю тетрадь как PDF. Логика.
Рабочая тетрадь, записи по учебнику «Логика» С.Н. Виноградов, А.Ф. Кузьмин. — 8-е изд. — Москва: 1954 — 174 c. Скачать PDF рабочую тетрадь с ответами на вопросы по логике: Скачать PDF