1.7 Теорема Гаусса

Вычисление напряжённости поля можно значительно упростить.

Рассмотрим поток вектора напряжённости через сферическую поверхность радиуса $r$, охватывающую положительный точечный заряд $q$, находящийся в её центре. (см. рис. 10) Как Вам известно, площадь поверхности сферы $S = 4 \pi r^2$. Тогда учитывая, что линии напряжённости в данном случае — радиальные прямые, то есть всегда перпендикулярны поверхности, получим: \[ \Phi_E = \oint\limits_S E_n \mathrm{d} S = \dfrac{q}{4 \pi \varepsilon_0 r^2} 4 \pi r^2 = \dfrac{q}{\varepsilon_0} \]

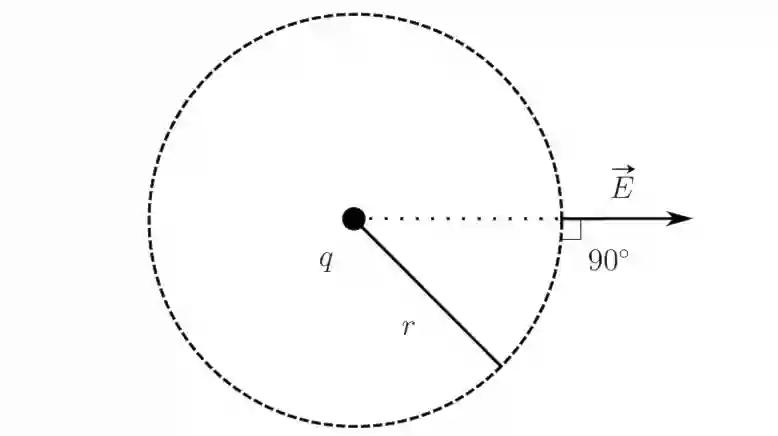
Доказано, что этот результат справедлив для любой замкнутой поверхности произвольной формы, охватывающей заряд. В этом диалоге с Вами, я позволю себе пропустить данное доказательство.

Если расположить заряд рядом с замкнутой поверхностью, то есть снаружи, то поток через замкнутую поверхность будет равен нулю. Этот факт можно объяснить тем, что каждая силовая линия пересекает замкнутую поверхность дважды. Сначала входит в область ограниченную поверхностью, потом выходит из неё. (Например см. рис. 11)

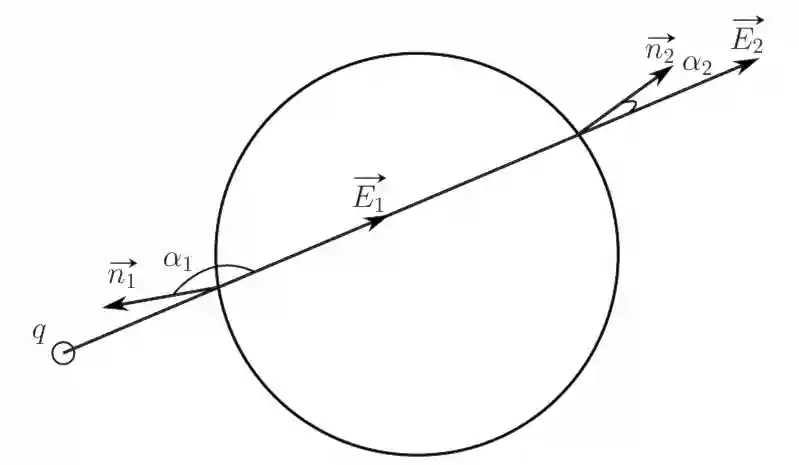
Как видно из рисунка 11, входящий поток будет равен: \[ \mathrm{d} \Phi_{E1} = E_1 \cdot \mathrm{d} S \cos \alpha_1 \] выходящий поток будет равен: \[ \mathrm{d} \Phi_{E2} = E_2 \cdot \mathrm{d} S \cos \alpha_2 \] так как $E_1 = E_2$, и площади элементарных площадок тоже одинаковы, то полный входящий и полный выходящий потоки через обе оболочки равны по модулю. Так как угол $\alpha_1$ — тупой, а угол $\alpha_2$ — острый, то входящий и выходящий поток противоположны по знаку, итого: \[ \Phi_{E2} = - \Phi_{E1} \] Значит полный поток через замкнутую поверхность от заряда расположенного снаружи равен: \[ \Phi_E = \Phi_{E1} + \Phi_{E2} = \Phi_{E1} - \Phi_{E1} = 0 \]

Данный пример не является строгим доказательством, но очень нагляден.

Рассмотрим общий случай произвольной поверхности, окружающей $n$ зарядов. Согласно принципу суперпозиции напряжённость поля $\vec{E}$, создаваемого всеми зарядами, равна сумме напряжённостей $\vec{E_i}$ , создаваемых каждым зарядом в отдельности. Так как интеграл от суммы равен сумме интегралов, то получим: \[ \Phi_E = \oint\limits_S \vec{E} \cdot \vec{\mathrm{d} S} = \oint\limits_S \left( \sum\limits_{i=1}^n \vec{E_i} \right) \cdot \vec{ \mathrm{d} S } = \] \[ = \sum\limits_{i=1}^n \oint\limits_S \vec{E_i} \vec{ \mathrm{d} S } = \sum\limits_{i=1}^n \dfrac{q_i}{\varepsilon_0} = \dfrac{1}{\varepsilon_0} \sum\limits_{i=1}^n q_i\]

Теорема Гаусса для электростатического поля в вакууме: поток вектора напряжённости электростатического поля $\Phi_E$ в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключённых внутри этой поверхности, делённых на электрическую постоянную $\varepsilon_0$. \[ \Phi_E = \oint\limits_S \vec{E} \cdot \vec{\mathrm{d} S} = \dfrac{1}{\varepsilon_0} \sum\limits_{i=1}^n q_i \]

Если заряд распределён в пространстве с объёмной плотностью $\rho = \dfrac{\mathrm{d} q}{\mathrm{d} V}$, то для того, чтобы найти сумму зарядов в пространстве, нужно проинтегрировать объёмную плотность по объёму. Теорема Гаусса примет следующий вид: \[ \Phi_E = \oint\limits_S \vec{E} \cdot \vec{\mathrm{d} S} = \dfrac{1}{\varepsilon_0} \int\limits_V \rho \mathrm{d} V \]