1.6 Принцип суперпозиции электростатических полей

К Кулоновским силам применим такой принцип: результирующая сила, действующая со стороны поля на пробный заряд равна векторной сумме сил, приложенных к пробному заряду со стороны каждого из зарядов, создающих электростатическое поле. Этот принцип называется принципом суперпозиции.

Принцип суперпозиции (наложения) электростатических полей.

\[ \vec{E} = \sum\limits_{i=1}^n \vec{E_i} \] Напряжённость результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряжённостей полей, создаваемых в данной точке каждым из зарядов в отдельности. (буква $n$ в формуле — количество зарядов создающих поле)

С помощью данной формулы можно рассчитать напряжённости любого поля, состоящего из системы неподвижных зарядов, представив поле в виде совокупности точечных зарядов.

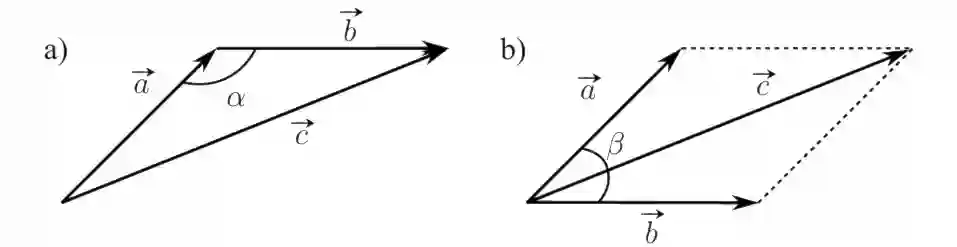
Геометрическое сложение векторов

Вспомним правило определения величины вектора $\vec{c}$ являющегося суммой двух векторов $\vec{a}$ и $ \vec{b} $. Из теоремы косинусов следует, что (см. рис. 9.a): \[ | \vec{c} | = \sqrt{a^2 + b^2 - 2ab \cos \alpha}\] Рассмотрим другой случай, расположим вектора так, чтобы их начало совпадало. Тогда угол между ними $\beta = 180 - \alpha$, получим (см. рис. 9.b): \[ | \vec{c} | = \sqrt{a^2 + b^2 + 2ab \cos \beta} \]