1.5 Поток вектора напряжённости
Поток вектора напряжённости $\vec{E}$. Чтобы с помощью линий напряжённости можно было охарактеризовать не только направление, но и значение напряжённости электростатического поля, линии проводят с определённой густотой: число линий напряжённости, пронизывающих единицу площади поверхности, перпендикулярную линиям напряжённости, должно быть равно модулю вектора напряжённости. Обозначу число линий буквой $N$, тогда получим, что напряжённость в области некоторой площадки, перпендикулярной силовым линиям равна: $ E = \dfrac{N}{\mathrm{d} S_{ \perp }} $
Соответственно, там где линий напряжённости больше, там и выше значение напряжённости.
Мы можем посчитать число линий напряжённости, пронизывающих некоторую площадку $\mathrm{d} S$, расположенную случайным образом. Число линий будет равно: \[ N = E \cdot \mathrm{d} S \cos \alpha = E_n \mathrm{d} S, \] где $\alpha$ — угол между нормалью к площадке $\vec{n}$ и вектором напряжённости $\vec{E}$, а $E_n$ — проекция вектора $\vec{E}$ на $\vec{n}$. (Вектор нормали $\vec{n}$ — единичный вектор, перпендикулярный площадке $\mathrm{d} S$). (см. рис. 8)
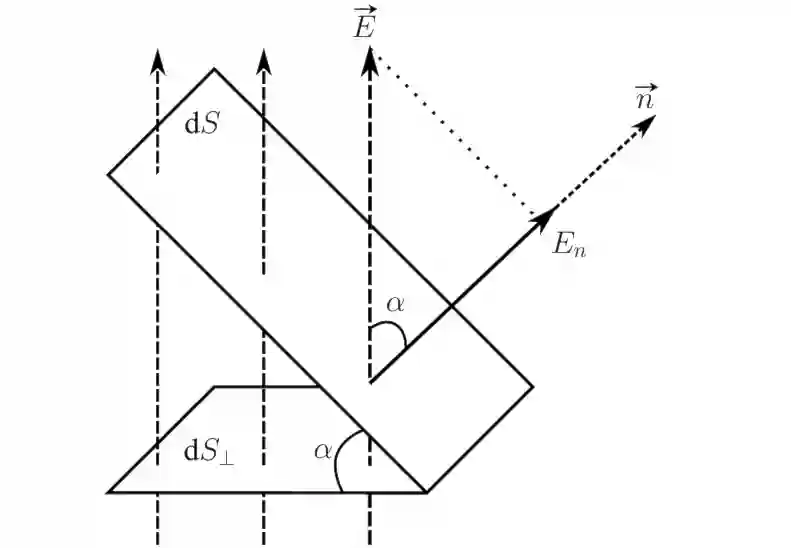
Введём новую величину, показывающую сколько линий напряжённости проходит сквозь произвольную площадку площади $\mathrm{d} S$: \[ \mathrm{d} \Phi_E = E \cdot \mathrm{d} S_{ \perp } = E \cdot \mathrm{d} S \cos \alpha = E_n \mathrm{d} S = \vec{E} \cdot \vec{ \mathrm{d} S } \]
Величина $\mathrm{d} \Phi_E$ называется потоком вектора напряжённости через площадку $\mathrm{d} S$ \[ \mathrm{d} \Phi_E = \vec{E} \cdot \vec{ \mathrm{d} S } \] Здесь $\vec{ \mathrm{d} S } = \mathrm{d} S \cdot \vec{n} $ — вектор, модуль которого равен $\mathrm{d} S$, а направление совпадает с направлением нормали $\vec{n}$ к площадке.
Мы можем найти количество линий напряжённости, пронизывающих любую поверхность, любой площади и формы. Для этого необходимо разбить поверхность на элементарные области $\mathrm{d} S$ , а далее вычислить поток для каждой из этих элементарных областей, пологая, что в пределах малой области поверхность можно считать плоской, а поле — однородным.
Полный поток $\Phi_E$ через всю произвольную поверхность находится суммированием (интегрированием) всех элементарных потоков.
Тогда поток вектора напряжённости $\vec{E}$ сквозь произвольную замкнутую поверхность $S$, будет равен: \[ \Phi_E = \oint\limits_S E_n \mathrm{d} S = \oint\limits_S \vec{E} \cdot \vec{ \mathrm{d} S } \] в данном случае окружность на интеграле обозначает, что поверхность замкнута.