1.4 Напряжённость электростатического поля
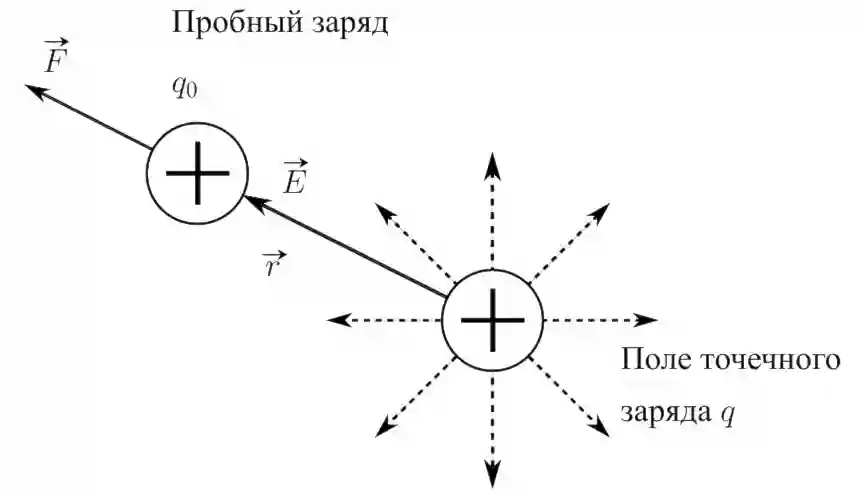
Поместив в поле так называемый пробный заряд $q_0$ — являющийся единичным положительным зарядом, мы можем определить по закону Кулона, какая сила будет действовать на него в данной точке со стороны всей системы зарядов поля. \[ \vec{E} = \dfrac{\vec{F}}{q_0} \]
Напряжённость электростатического поля $\vec{E}$ — векторная физическая величина, показывающая какая сила действует на единичный положительный заряд $q_0$, помещённый в данную точку поля.
Единица напряжённости электростатического поля — Ньютон на Кулон (Н/Кл): \[ 1 \dfrac{\text{Н}}{\text{Кл}} = 1 \dfrac{\text{В}}{\text{м}}, \] где В (вольт) — единица потенциала электростатического поля.
Напряжённость поля точечного заряда вычисляется по формуле: \[ \vec{E} = \dfrac{1}{4 \pi \varepsilon_0 \varepsilon} \dfrac{q}{r^2} \dfrac{\vec{r}}{r} \] где $\vec{r}$ — радиус-вектор, с началом в $q$ и концом в $q_0$. В вакууме $\varepsilon = 1$.
В скалярной форме: \[ E = \dfrac{1}{4 \pi \varepsilon_0 \varepsilon} \dfrac{q}{r^2} \]
Направление вектора напряжённости $\vec{E}$ совпадает с направлением силы, действующей на положительный пробный заряд. (например см. рис. 5)
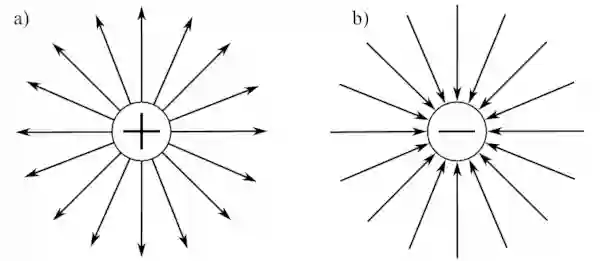
Если поле создаётся положительным зарядом, то вектор $\vec{E}$ направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда). (см. рис. 6.a)
Если поле создаётся отрицательным зарядом, то вектор $\vec{E}$ направлен к заряду (притяжение). (см. рис. 6.b)
Графическое представление электростатического поля. Электростатическое поле изображают с помощью линий напряжённости (силовых линий).
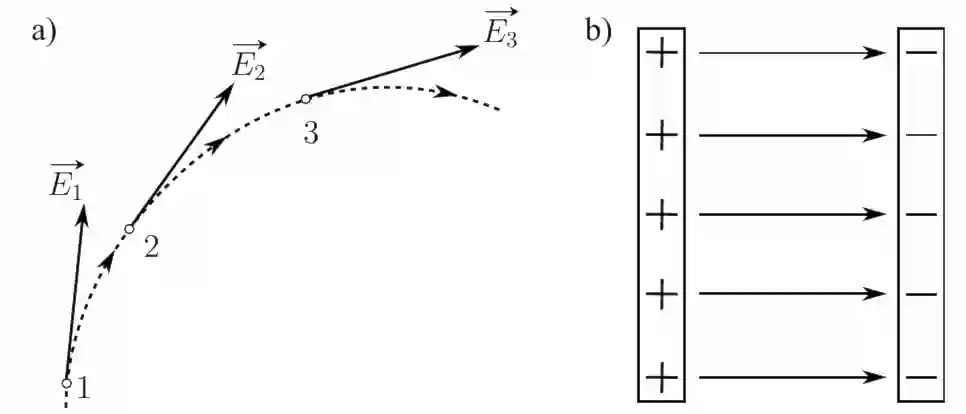
Линии напряжённости — это линии, касательные к которым в каждой точке совпадают с направлением вектора $\vec{E}$ . Линиям напряжённости приписывается направление, совпадающее с направлением вектора напряжённости (см. рис. 7.a). Так как в данной точке пространства вектор напряжённости имеет лишь одно направление, то линии напряжённости никогда не пересекаются.
Для однородного поля (когда вектор напряжённости в любой точке постоянен по модулю и направлению) линии напряжённости параллельны вектору напряжённости. (см. рис. 7.b)
Если поле создаётся точечным зарядом, то линии напряжённости — радиальные прямые, выходящие из заряда, если он положителен, и входящие в него, если заряд отрицателен (см. рис. 6).