1.19 Условия на границе раздела двух диэлектрических сред

Рассмотрим рисунок 30.a, имеются два диэлектрика с проницаемостями $\varepsilon_1$ и $\varepsilon_2$. При отсутствии на границе двух диэлектриков свободных зарядов, циркуляция вектора $\vec{E}$ по контуру: \[ \oint\limits_{ABCDA} \vec{E} \vec{\mathrm{d} l} = 0 \] Пусть в нашем примере $AB = l, CD = l, BC \to 0, DA \to 0$, тогда: \[ \oint\limits_{ABCDA} \vec{E} \vec{\mathrm{d} l} = \int\limits_{AB} \vec{E_1} \vec{\mathrm{d} l} + \int\limits_{BC} \vec{E_{\text{бок1}}} \vec{\mathrm{d} l} + \int\limits_{CD} \vec{E_2} \vec{\mathrm{d} l} + \int\limits_{DA} \vec{E_{\text{бок2}}} \vec{\mathrm{d} l} =\] \[\oint\limits_{ABCDA} \vec{E} \vec{\mathrm{d} l} = (\vec{E_1} \vec{AB} ) + 0 + (\vec{E_2} \vec{CD} ) + 0 =\] Так как вектора $\vec{AB}$ и $\vec{CD}$ противоположно направлены, угол между направлениями $\vec{E_2}$ и $\vec{CD}$ больше $90^{\circ}$, то появляется знак минус: \[ \oint\limits_{ABCDA} \vec{E} \vec{\mathrm{d} l} = E_1 \sin \alpha_1 l - E_2 \sin \alpha_2 l =E_{\tau 1} l - E_{\tau 2} l = 0 \] Поэтому: \[ E_{\tau 1} = E_{\tau 2} \] Учитывая, что $D = \varepsilon_0 \varepsilon E$, получим: \[ \dfrac{D_{\tau 1}}{D_{\tau 2}} = \dfrac{\varepsilon_1}{\varepsilon_2} \]

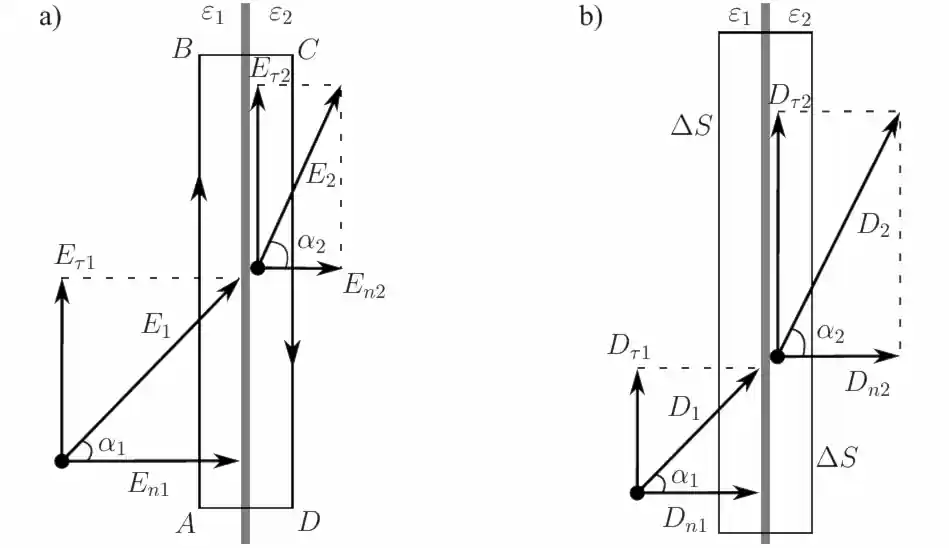
Рассмотрим рисунок 30.b. Найдём полный поток вектора электрического смещения $\vec{D}$ через цилиндр ничтожно малой высоты $h \to 0$. Прямоугольник на рисунке 30.b − это сечение цилиндра. \[ \Phi_D = \Phi_{D1} + \Phi_{D2} + \Phi_{D \text{бок}} \] Поток через боковую поверхность равен нулю: $\Phi_{D \text{бок}} = 0$, так как $h \to 0$. А по теореме Гаусса полный поток вектора $\vec{D}$ равен нулю, так как свободные заряды отсутствуют. Таким образом, имеем: \[ \Phi_D = \Phi_{D1} + \Phi_{D2} = 0 \] Так как вектора нормали $\vec{n_1}$ и $\vec{n_2}$ противоположно направлены, угол между направлениями $\vec{D_1}$ и $\vec{n_1}$ больше $90^{\circ}$, то появляется знак минус: \[ \Phi_D = - D_1 \Delta S \cos \alpha_1 + D_2 \Delta S \cos \alpha_2 = 0 \] \[ D_{n1} \Delta S - D_{n2} \Delta S = 0 \] \[ D_{n1} = D_{n2} \] Учитывая, что $E = \dfrac{D}{\varepsilon_0 \varepsilon}$, получим: \[ \dfrac{E_{n1}}{E_{n2}} = \dfrac{\varepsilon_2}{\varepsilon_1} \] При пересечении границы раздела двух диэлектрических сред тангенциальная составляющая вектора $\vec{E} \; (E_{\tau})$ и нормальная составляющая вектора $\vec{D} \; (D_n)$ сохраняются, а нормальная составляющая вектора $\vec{E} \; (E_n)$ и тангенциальная составляющая вектора $\vec{D} \; (D_{\tau})$ претерпевают скачок.