1.14.6 Поле равномерно заряженной бесконечной нити (цилиндра).

Рассмотрим бесконечный цилиндр радиуса $R$ равномерно положительно заряженный с линейной плотностью $\tau = \dfrac{\mathrm{d} q}{\mathrm{d} l}$. Если принять, что $R$ очень мало, $R \to 0$, то можно считать этот цилиндр тонкой нитью. В таком случае нас интересует только внешнее поле этого цилиндра.

Линии напряжённости будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. (см. рис. 25)

В качестве Гауссовой поверхности выберем цилиндр радиуса $r$ и длиной образующей $l$, имеющий общую ось с заряженным цилиндром.

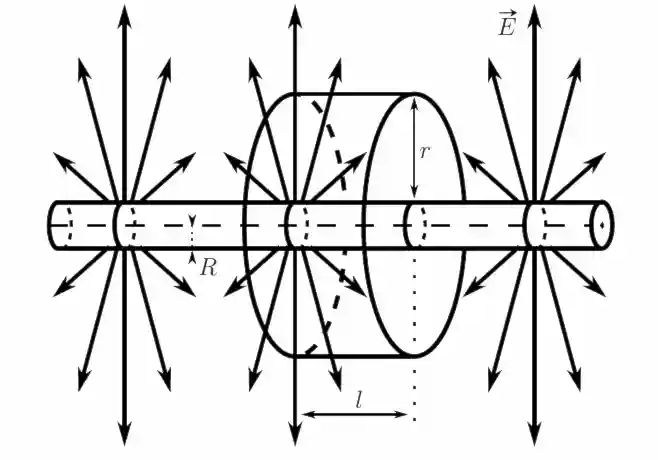
Основания этого цилиндра будут параллельны линиям напряжённости, поэтому поток через них равен нулю.

Поток через боковую поверхность равен $E \cdot 2 \pi r l$ При $r>R$ цилиндр охватывает заряд, равный $q = \tau l$. По теореме Гаусса \[ 2 \pi r l E = \dfrac{\tau l}{\varepsilon_0} \] откуда \[ E = \dfrac{1}{2 \pi \varepsilon_0} \dfrac{\tau}{r} \] Разность потенциалов для точек 1 и 2 лежащих снаружи заряженного цилиндра соответственно на расстояниях $r_1$ и $r_2$ от оси цилиндра $(r_1 > R, r_2 > R)$: \[ \phi_1 - \phi_2 = \int\limits_1^2 \vec{E} \vec{\mathrm{d} l} \] далее учитывая, что силовые линии $\vec{E}$ направлены по радиусам, так же как и расстояния $r_1$ и $r_2$, то обозначим через $\mathrm{d} r$ проекцию $\vec{\mathrm{d} l}$ на $\vec{E}$. \[ \phi_1 - \phi_2 = \int\limits_{r_1}^{r_2} E \mathrm{d} r = \dfrac{\tau}{2 \pi \varepsilon_0} \int\limits_{r_1}^{r_2} \dfrac{\mathrm{d} r}{r} \] \[ \phi_1 - \phi_2 = \dfrac{\tau}{2 \pi \varepsilon_0} \ln \dfrac{r_2}{r_1} \]