1.14.5 Поле объёмно заряженного шара.

Рассмотрим шар радиуса $R$. Положительный заряд $q$ равномерно распределён в вакууме по объёму шара с объёмной плотностью \[ \rho = \dfrac{q}{V} = \dfrac{q}{\dfrac{4}{3} \pi R^3} \] Центр шара является центром симметрии поля. Будем рассуждать аналогично предыдущему примеру. Введём сферу радиуса $r$ и примем её за Гауссову поверхность.

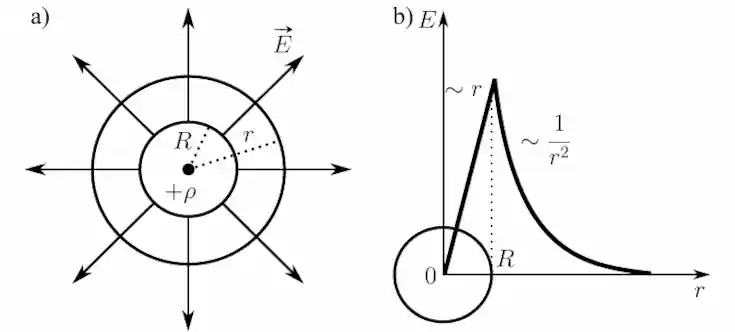
Для поля вне шара $(r>R)$ получаем тот же результат, что и в случае сферической поверхности: \[ E = \dfrac{1}{4 \pi \varepsilon_0} \dfrac{q}{r^2} \] \[ \phi = \dfrac{q}{4 \pi \varepsilon_0 r} \] \[ \phi_1 - \phi_2 = \dfrac{q}{4 \pi \varepsilon_0} \left( \dfrac{1}{r_1} - \dfrac{1}{r_2} \right) \] Найдём напряжённость и потенциал поля самого шара. $r = R$: \[ E = \dfrac{1}{4 \pi \varepsilon_0} \dfrac{q}{R^2} = \dfrac{\rho R}{3 \varepsilon_0} \] \[ \phi = \dfrac{q}{4 \pi \varepsilon_0 R} = \dfrac{\rho R^2}{3 \varepsilon_0} \] Рассчитаем напряжённость и потенциал поля внутри шара. Сфера радиусом $r < R$ охватывает заряд $q = \dfrac{4}{3} \pi r^3 \rho$. По теореме Гаусса: \[ 4 \pi r^2 E = \dfrac{q}{\varepsilon_0} = \dfrac{4 \pi r^3 \rho}{3 \varepsilon_0} = \dfrac{r^3 q}{R^3 \varepsilon_0} \] откуда: \[ E = \dfrac{q r}{4 \pi \varepsilon_0 R^3} = \dfrac{\rho r}{3 \varepsilon_0} \] Разность потенциалов для точек 1 и 2 лежащих внутри шара соответственно на расстояниях $r_1$ и $r_2$ от центра шара $(r_1 < R, r_2 < R)$: \[ \phi_1 - \phi_2 = \int\limits_1^2 \vec{E} \vec{\mathrm{d} l} \] далее учитывая, что силовые линии $\vec{E}$ радиальны, так же как и расстояния $r_1$ и $r_2$, то обозначим через $\mathrm{d} r$ проекцию $\vec{\mathrm{d} l}$ на $\vec{E}$. \[ \phi_1 - \phi_2 = \int\limits_{r_1}^{r_2} E \mathrm{d} r = \dfrac{q}{4 \pi \varepsilon_0 R^3} \left. \dfrac{r^2}{2} \right|^{r_2}_{r_1} \] \[ \phi_1 - \phi_2 = \dfrac{q}{8 \pi \varepsilon_0 R^3} (r_2^2 - r_1^2) \]