1.14.4 Поле равномерно заряженной сферической поверхности.

Рассмотрим сферическую поверхность радиуса $R$ с общим положительным зарядом $q$, то есть равномерно заряженную с поверхностной плотностью $\sigma = \dfrac{q}{4 \pi R^2}$.

Система зарядов и само поле расположены центрально-симметрично относительно центра сферы, линии напряжённости направлены радиально.

Введём ещё одну сферу, имеющую общий центр с заряженной сферой, но другого радиуса, радиуса $r$. Примем эту новую сферу радиуса $r$ Гауссовой поверхностью.

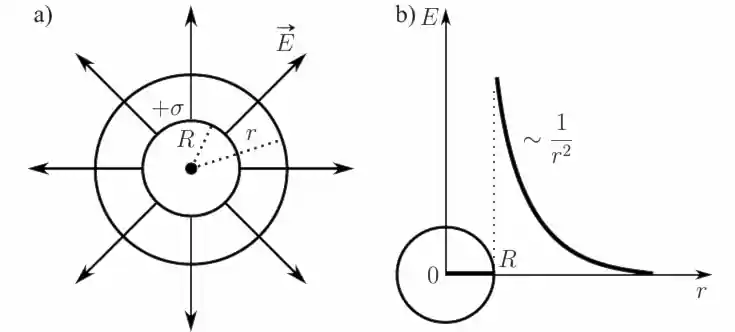
Если $r \geq R$, то внутрь поверхности попадает весь заряд $q$. По теореме Гаусса: \[ 4 \pi r^2 E = \dfrac{q}{\varepsilon_0}, \] откуда \[ E = \dfrac{1}{4 \pi \varepsilon_0} \dfrac{q}{r^2} = \dfrac{\sigma R^2}{\varepsilon_0 r^2}, \; (r \geq R) \]

Если $r < R$, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферы $E = 0$.

Разность потенциалов между точками 1 и 2, лежащими соответственно на расстояниях $r_1$ и $r_2$ от центра сферы снаружи её поверхности $(r_1 > R, r_2 > R)$, равна: \[ \phi_1 - \phi_2 = \int\limits_1^2 \vec{E} \vec{\mathrm{d} l}\] далее $\mathrm{d} r$ — проекция $\vec{\mathrm{d} l}$ на $\vec{E}$. Так как расстояния $r_1$ и $r_2$ также как и силовые линии лежат на радиальных прямых, то получим \[ \phi_1 - \phi_2 = \int\limits_{r_1}^{r_2} E \mathrm{d} r = \int\limits_{r_1}^{r_2} \dfrac{1}{4 \pi \varepsilon_0} \dfrac{q}{r^2} \mathrm{d} r \] \[ \phi_1 - \phi_2 = \dfrac{q}{4 \pi \varepsilon_0} \left( \dfrac{1}{r_1} - \dfrac{1}{r_2} \right) \] Если принять $r_1 = r$ и $r_2 \to \infty$ (на бесконечном отдалении потенциал $\phi_2 = 0$), то получим потенциал поля вне сферической поверхности \[ \phi = \dfrac{1}{4 \pi \varepsilon_0} \dfrac{q}{r} \] Вне заряженной сферы поле точно такое же, как поле точечного заряда $q$, если бы он находился в центре сферы.

Потенциал — функция непрерывная, значит, внутри заряженной сферы, где нет поля, потенциал должен совпадать с потенциалом на поверхности сферы $r = R$. Внутри заряженной сферы потенциал постоянен и равен потенциалу на поверхности сферы. \[ \phi = \dfrac{q}{4 \pi \varepsilon_0 R} = \dfrac{\sigma R}{\varepsilon_0} \]