1.14.3 Поле двух бесконечных параллельных разноимённо заряженных плоскостей с равными по абсолютному значению поверхностными плотностями зарядов

Рассмотрим две бесконечные параллельные плоскости находящиеся на расстоянии $d$ друг от друга, первая из которых имеет поверхностный заряд $+ \sigma$, а вторая $- \sigma$.

Из предыдущего примера следует, что векторы напряжённости $\vec{E_1}$ и $\vec{E_2}$ первой и второй плоскостей равны по модулю и всюду направлены перпендикулярно плоскостям. $E_1 = E_2$ Поэтому в пространстве вне плоскостей они компенсируют друг друга так как направлены в противоположные стороны, а в пространстве между плоскостями суммируются так как имеют одинаковое направление.

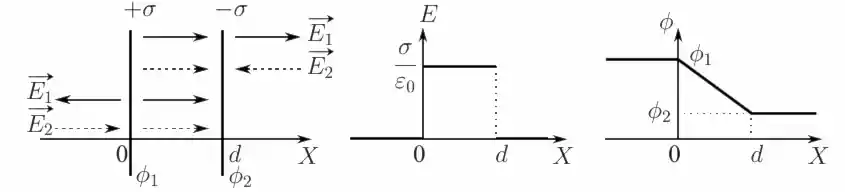
Напряжённость между плоскостями равна: \[ E = E_1 + E_2 = \dfrac{\sigma}{2 \varepsilon_0} + \dfrac{\sigma}{2 \varepsilon_0} \] \[ E = \dfrac{\sigma}{\varepsilon_0} \] или в диэлектрике: \[ E = \dfrac{\sigma}{\varepsilon \varepsilon_0} \] Поле между плоскостями однородное. Разность потенциалов между плоскостями вычисляется способом, аналогичным предыдущему примеру: \[ \phi_1 - \phi_2 = E (x_2 - x_1) = \dfrac{\sigma}{\varepsilon_0} (d - 0) \] \[ \phi_1 - \phi_2 = \dfrac{\sigma d}{\varepsilon_0} \] или в диэлектрике: \[ \phi_1 - \phi_2 = \dfrac{\sigma d}{\varepsilon \varepsilon_0} \]