1.14.1 Электростатическое поле электрического диполя.

Электрическим диполем (или двойным электрическим полюсом) называется система двух равных по модулю разноимённых точечных зарядов $(+q, -q)$, отстоящих друг от друга на расстоянии $l$. В случае, когда расстояние от диполя до точки наблюдения значительно больше расстояния между полюсами диполя $(r > > l)$, такой диполь называют точечным. Мы будем рассматривать точечные диполи.

Плечо диполя $\vec{l}$ — это вектор, направленный по оси диполя от отрицательного заряда к положительному, и равный расстоянию между ними.

Электрический момент диполя $\vec{p_e}$ — вектор, совпадающий по направлению с плечом диполя и равный произведению модуля заряда $|q|$ на плечо $\vec{l}$: \[ \vec{p_e} = |q| \vec{l} \]

Напряжённость поля диполя на продолжении оси диполя

Рассмотрим точку находящуюся на продолжении оси диполя, например точку A. (см. рис. 18) Если поместить в точку A пробный положительный заряд, то отрицательный полюс диполя будет притягивать пробный заряд, а положительный отталкивать, получим два противоположно направленных вектора на одной прямой, вектор напряжённости для этого заряда будет геометрической суммой полученных векторов: \[ E_A = E_+ - E_- \]

Потенциал поля в точке A по принципу суперпозиции потенциалов, будет равен алгебраической сумме потенциалов от полей образованных полюсами диполя: \[ \phi_A = \phi_+ + \phi_- \]

Пусть $r$ — расстояние от середины оси диполя до точки A. Тогда, учитывая что $r > > l$, подставим значения расстояний от точки A до полюсов диполя (учитывая недостающие половинки $l$ ) в формулу напряжённости:

\[ E_A = \dfrac{1}{4 \pi \varepsilon_0} \dfrac{q}{ \left( r - \dfrac{l}{2} \right)^2 } - \dfrac{1}{4 \pi \varepsilon_0} \dfrac{q}{ \left( r + \dfrac{l}{2} \right)^2 } = \] \[ = \dfrac{q}{4 \pi \varepsilon_0} \dfrac{ \left( r + \dfrac{l}{2} \right)^2 - \left( r - \dfrac{l}{2} \right)^2 }{ \left( r^2 - \left( \dfrac{l}{2} \right)^2 \right)^2 } = \] \[ = \dfrac{q}{4 \pi \varepsilon_0} \dfrac{r^2 + rl + \dfrac{l^2}{4} - (r^2 - rl + \dfrac{l^2}{4})}{r^4 - 2 \cdot r^2 \cdot \dfrac{l^2}{4} + \left( \dfrac{l}{2} \right)^4 } \approx \dfrac{q}{4 \pi \varepsilon_0} \dfrac{2rl}{r^4} \approx \] \[ E_A \approx \dfrac{1}{4 \pi \varepsilon_0} \dfrac{2ql}{r^3} = \dfrac{1}{4 \pi \varepsilon_0} \dfrac{2 p_e}{r^3} \] Так же вычислим потенциал: \[ \phi_A = \dfrac{1}{4 \pi \varepsilon_0} \cdot \dfrac{q}{r - \dfrac{l}{2}} - \dfrac{1}{4 \pi \varepsilon_0} \cdot \dfrac{q}{r + \dfrac{l}{2} } \] здесь $q$ — это значение заряда создающего поле, то есть полюса диполя, поэтому у положительного полюса потенциал со знаком плюс, а у отрицательного со знаком минус.

Потенциал поля диполя на продолжении оси диполя равен:

\[ \phi_A = \dfrac{q}{4 \pi \varepsilon_0} \dfrac{r + \dfrac{l}{2} - r + \dfrac{l}{2}}{r^2 - \dfrac{l^2}{4}} \approx \] \[ \phi_A \approx \dfrac{1}{4 \pi \varepsilon_0} \dfrac{ql}{r^2} = \dfrac{1}{4 \pi \varepsilon_0} \dfrac{p_e}{r^2} \]

Напряжённость поля в точке на перпендикуляре, восстановленном к оси диполя из его середины

Рассмотрим пробный положительный заряд в точке B расположенной на перпендикуляре к оси диполя, проведённом из середины оси.

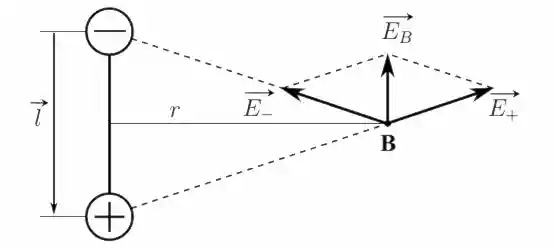
Так как точка B расположена на одинаковых расстояниях от обоих полюсов, равном $\sqrt{r^2 + \left( \dfrac{l}{2} \right)^2 }$ то, учитывая $r > > l$: \[ E_+ = E_- = \dfrac{1}{4 \pi \varepsilon_0} \dfrac{q}{r^2 + \left( \dfrac{l}{2} \right)^2} \approx \dfrac{1}{4 \pi \varepsilon_0} \dfrac{q}{r^2} \] Из подобия треугольников и условия что $r$ гораздо больше $l$ следует: \[ \dfrac{E_B}{E_+} \approx \dfrac{l}{r} \] поэтому \[ E_B \approx (E_+) \dfrac{l}{r} \] \[ E_B \approx \dfrac{1}{4 \pi \varepsilon_0} \dfrac{ql}{r^3} = \dfrac{1}{4 \pi \varepsilon_0} \dfrac{p_e}{r^3} \]

Точка B равноудалена от полюсов диполя, поэтому потенциал поля в точке B равен нулю. \[ \phi_B = 0 \]

Вектор $\vec{E_B}$ направлен противоположно вектору $\vec{l}$.

Диполь во внешнем электрическом поле.

Во внешнем электрическом поле на концы диполя действует пара сил, которая стремиться повернуть диполь таким образом, чтобы электрический момент $\vec{p_e}$ диполя развернулся вдоль направления поля $\vec{E}$. Кулоновские силы тянут положительный полюс вперёд по направлению вектора напряжённости $\vec{E}$ , а отрицательный полюс назад. (см. рис. 20.a)

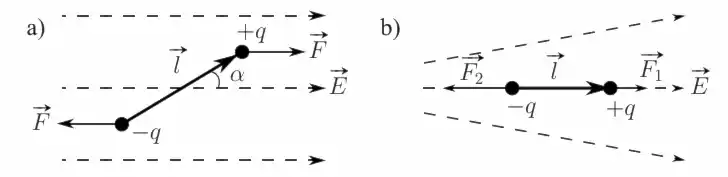
Во внешнем однородном поле момент пары сил, по свойству момента пары сил равен: \[ \vec{M} = [\vec{l}, \vec{F}] = q[\vec{l}, \vec{E}]\] \[ \vec{M} = [\vec{p_e}, \vec{E}] \] \[ M = ql E \sin \alpha \]

Во внешнем неоднородном поле силы, действующие на концы диполя, неодинаковы и их результирующая стремится передвинуть диполь в область поля с большей напряжённостью — диполь втягивается в область более сильного поля. (см. рис. 20.b)