1.13 Эквипотенциальные поверхности

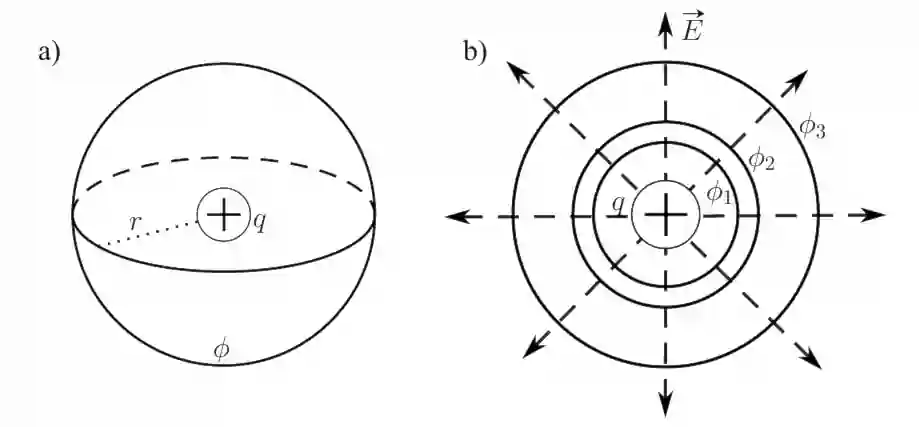
Для графического изображения распределения потенциала используются эквипотенциальные поверхности – поверхности, во всех точках которых потенциал имеет одно и то же значение. Например рассмотрим точечный положительный заряд $q$, для него потенциал вычисляется как: $\phi = \dfrac{1}{4 \pi \varepsilon_0} \dfrac{q}{r}$, значит значение потенциала будет одинаковым во всех точках, расположенных на расстоянии $r$ от заряда $q$. Поэтому эквипотенциальная поверхность для точечного заряда — это концентрическая сфера. (см. рис. 14.a)

Эквипотенциальные поверхности обычно проводят так, чтобы разности потенциалов между двумя соседними эквипотенциальными поверхностями были одинаковы. Посмотрите напримере того же точечного заряда $q$ (см. рис. 14.b). На рисунке проведены сечения сферических поверхностей, проведены так, что соблюдается правило: $\phi_1 - \phi_2 = \phi_2 - \phi_3$

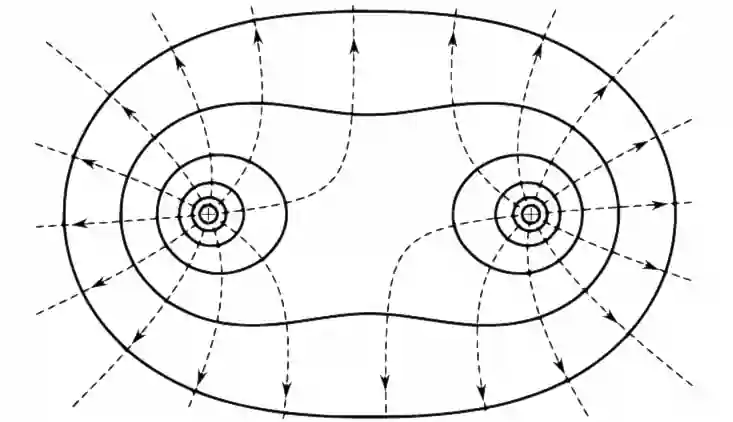
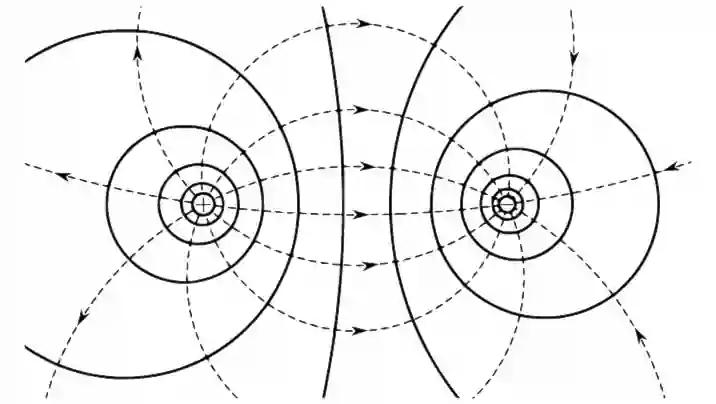
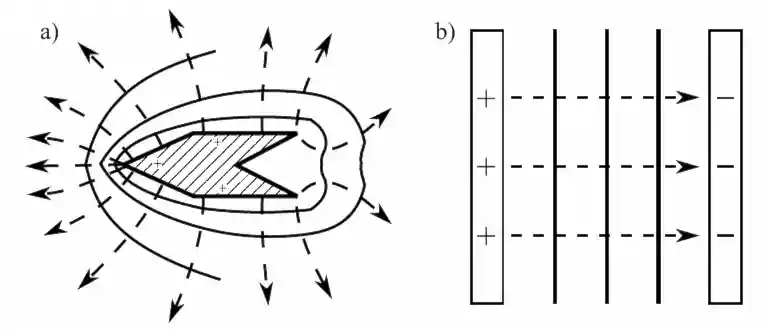
Если проводить эквипотенциальные поверхности таким образом, то их густота наглядно характеризует напряжённость поля в разных точках. Там, где эти поверхности расположены гуще, напряжённость поля больше.

На рисунках пунктиром изображены силовые линии, сплошными линиями — сечения эквипотенциальных поверхностей.

Пусть мы перемещаем пробный заряд по эквипотенциальной поверхности с потенциалом $\phi$ на вектор $\vec{\mathrm{d} l}$. Ранее мы уже сравнивали определение работы и потенциала и получили, что \[ \mathrm{d} \phi = - ( \vec{E} \cdot \vec{\mathrm{d} l} ) \] Так как эквипотенциальная поверхность проводится в тех точках, где потенциал одинаковый, то $\phi = \text{const}$, а значит $\mathrm{d} \phi = 0$ получаем, что: \[ \vec{E} \cdot \vec{\mathrm{d} l} = 0 \] скалярное произведение вектора напряжённости $\vec{E}$ и вектора перемещения по эквипотенциальной поверхности $\vec{\mathrm{d} l}$ равно нулю, когда $\cos \alpha = 0$, где $\alpha = 90^{\circ}$ угол между векторами.

Тем самым мы доказали, что:

Вектор напряжённости $\vec{E}$ всегда перпендикулярен эквипотенциальным поверхностям.

Вектор напряжённости $\vec{E}$ направлен в сторону убывания потенциала.